Craps Dice Odds
History – How To Play – Rules – Odds – Strategy – Pro’s Perspective
Craps is a table game played with dice that is highly popular in land-based casinos. Although it can be played at online casinos, it is more fun and exciting at land-based casinos. Whenever you enter a land-based casino, you will find a table that has players around it screaming and yelling numbers — this is the Craps table. There are two types of Craps. One is casino craps. In this game, players at the Craps table are all betting against the house or the casino, which is why it is called Casino Craps. The second kind is called Street Craps, which is where players play against each other — it used to be played in the streets, hence the name.
Craps is a game of pure luck as it all depends on the dice and the numbers that are rolled. In this game, players will place wagers on the outcome of the two thrown dice. A player who throws the dice is referred to as the shooter. After the dice have been rolled, players will be paid according to the outcome. Some wagers need more than one roll, while other wagers can be settled after one roll. In this tutorial, we are going to discuss the payouts and the different wagers that can be placed at the Craps table as well as the rules players will have to follow while playing at the table.
Feb 19, 2021 Each number pays the better odds between place and buy bets. I refer to these as 'buy bets.' They pay 7-6 on the 6 & 8, 7-5 on the 5 & 9, and 39-20 on the 4 & 10. Lay bets pay true odds, but player must prepay a 5% commission, based on the possible win. This works out to odds of 19-25 on the 6 & 8, 19-31 on the 5 & 9, and 19-41 on the 4 & 10. You’re welcome, thanks for the kind words. The probability of throwing the dice n times without a 7, and then throwing a 7, is (5/6) n.(1/6). The probability of throwing n non-sevens, without specifying the next throw would be (5/6) n. So the probability of throwing the dice at least four times without a seven would be (5/6) 4 =625/1296=0.4823.
Craps Dice Probability Chart. The best bet in craps after the first roll is the odds bet. Once a point is determined, players will be able to place an additional wager that is a multiple of the pass line bet. The multiple differs from one casino to another, but the most common is 2X.
Craps History
Evidence suggests Craps may have originated and evolved during the ancient Roman Empire. While in camp Roman soldiers used to carve the knuckles of pigs into cubes and would toss them over their shield. The term “To Roll the Bones” originated from this game. Other theories claim Craps originated in the Middle Ages with the people in the Arabian deserts as they used to play a game that was quite similar to Craps called Hazard or Azzahr.
The definitive rules of this game were founded in the early 1700′s by Montmort. The roll that had the lowest value was referred to as crabs. While many believe this is where Craps got its name from, others believe the word evolved from Crapeaud, which is the French word for toad. Other theories claim the French were trying to reclaim the game as their own and they took the English word Crabs and spelled it in French as Crabes. In the 1700′s, the game succeeded in crossing the Atlantic Ocean and reached Acadia, the French Colony.
In 1755, the French lost their colony and the people of Acadia relocated to Louisiana. They brought the French game Crabes to Louisiana, but the game had changed to Creps or Crebs. By the year 1842, Craps started to be the dominant term and is still the name that is prevalent to this day.
During World War II, the Street version of the game became very popular and was played by the soldiers who used their blankets as the gaming surface. There was no wall to stop the dice from rolling out so they used blanket rolls to prevent it.
It is also important to note that the Craps version in modern America was brought by in Bernard Xavier Philippe, who was not only a politician but a gambler too. His version of Craps had a flaw that allowed players to exploit the game by taking advantage of the wagering system or by using fixed dice. This problem was fixed by John H Winn who introduced a new wagering option: “Do Not Pass”. This wagering option is used to this day at any casino that offers craps to its players around the world.
How to Play Craps
As mentioned before, there are two types of Craps, we are going to discuss the gaming procedure of the most commonly played Craps version, Casino or Bank Craps. This version is played at casinos, this is why in this game, players will place wagers against the casino. The payoffs of the game may differ from one casino to the next.
In this game, players will take turns in rolling the dice. As previously mentioned the player throwing the dice is called “The Shooter”. Before the shooter throws the dice, players will place their chips on the bets they want. They will find the different bets on a piece of green cloth; this piece of cloth has different available bets printed on it. Players can therefore easily place their chips on the bets they want to wager on. Players can usually go ahead and place their chips but there are some wagers that require players to ask the croupiers before putting them.
In order for a Craps player to get the chance to throw the dice as the shooter, he has to be active at the table by placing bets on either the Pass line or the Do Not Pass line wagers. These bets are also sometimes referred to as Right & Wrong or Win and Don’t Win bets.
Players will roll the dice and keep passing it on in a clockwise direction. The player who is throwing the dice, the shooter, will roll his dice until he loses by getting a 7 or until his round is completed. The dealer in this game, also known as the Stickman is the person who represents the casino. He is called a Stickman because he uses a stick to collect the chips and move the dice around. The Stickman will present the shooter with 5 different dice and the shooter chooses 2 of them. The remaining dice will be placed in a bowl.
There are numerous bet types that can be placed at the Craps table; we are going to discuss the most common one below, the Line Wager. The line wager contains two bets; they are called the Pass Line and the Do Not Pass line wagers. The first one is a bet that the shooter could win.
If the first roll which is also referred to as the come out dice roll lands on either a 7 or an eleven, then the dice shooter will win. If the dice is equal to 2, three, or 12, then shooter will lose. On the other hand, if the dice has any other outcome than the ones mentioned, this value will be called “Point”. In this case, the shooter will have to throw the dice again.
If he succeeds in rolling the point value before rolling a 7, he will win but if he rolls a 7 before he rolls the Point value, he will lose. The other bet is called the Do Not Pass wager, it is the exact opposite. Both bets pay 1:1.
Craps Rules
The rules at the Craps table include the wagers and the payouts. Apart from these basic rules, there are also some other unwritten rules that casinos implement at the Craps table. If you are a new player, after getting to know the basic payouts, rules and gaming procedure, you should also get to know these etiquette rules because you will be expected to abide by them at any casino.
Some of these rules are concerned with the security of each casino, including the following:
1. You are not permitted to handle the dice with both your hands. This includes shaking the dice in your hands before you throw them. Players are also expected to keep their hands on the surface of the craps table while they are handling the dice.
2. The shooter is required to throw the dice so they hit the other side of the table. Rolls that do not reach the other wall of the Craps table are called Mellenberg Rolls. Some casinos allow these rolls if they get past half the distance to the other wall. Any dice rolls that do not get past half the distance will have to be repeated because these short rolls can be controlled to somw extent.
3. Players should toss the dice on the table. Not slide them.
4. If the thrown dice by some chance hits other players or the hand of the dealer and still lands on the table, it can be counted provided that the players have not interfered with the rolled dice. Some casinos may deem these as no rolls and request the player re-roll the dice.
5. At some casinos, players will be able to call bets. Calling bets means they can start placing bets while they are waiting for their chips — they will call the bet and place it when they get the chips. Casinos that don’t allow such bets will have the words “No Call Bets” printed on the table of the game.
6. Casinos have the right to ask Craps players to leave the table at any given time without having to give any specific reason.
7. Do no toss chips on the craps table. Place them slowly.
8. Whenever players are offered to be the shooter, they are allowed to hand it to any other players at the table.
9. When players place service bets, which are bets that the dealers place on their behalf, they should tip them.
10. Players will tip dealers by throwing the tip on the table and saying “For the Boys” or “For the Dealers.” It works both for male and female dealers.
Craps Odds
Understanding and knowing the odds of the dice to get a certain outcome is the essence of Craps. If you are going to place real money wagers at a Craps table, it is essential for you to remember these odds. First of all, you will have a slight disadvantage when you place the Pass Line wager: the odds of winning are 970 out of 1980 times. In other words, the edge of the house for this wager equals 1.414 percent.
You can find the different bets that can be found at casinos, as well as their odds and the house advantage of each wager illustrated below:
The Pass Line wager has odds of 251 to 244, which is why players will be paid even money for this bet. The house advantage for this bet equals 1.414 percent. A Do Not Pass wager has odds of 976 to 949. It also pays even money and the house advantage equals 1.404 percent.
For Pass Line Bets:
– Betting on four or ten has odds of 2 to 1 and it pays out on the same rate, 2:1.
– Betting on five or nine has odds of 3 to 2 and it pays out on the same rate, 3:2.
– Betting on six or eight has odds of 6 to 5 and it pays out on the same rate, 6:5.
All of these bets have the same house advantage that is equal to 4.76 percent.
For Do No Pass Line Bets:
– Betting on four or ten has odds of 1 to 2 and it pays out on the same rate, 1:2. The house advantage is equal to 2.44 percent.
– Betting on five or nine has odds of 2 to 3 and it pays out on the same rate, 2:3. The house advantage is equal to 3.23 percent.
– Betting on six or eight has odds of 5 to 6 and it pays out on the same rate, 5:6. The house advantage is equal to 4 percent.
For Field Bets:
– Betting on 3, 4, 9, 10 or 11 pays 1:1
– Betting on 2 or 12 pays 2:1
All of these bets have odds of 5:4 and has a house advantage that is equal to 2.78%.
For One-Roll Bets:
– Any Seven has odds of 5 to 1, pays 4:1 and it has a house edge of 16.9 percent.
– Any Craps has odds of 8 to 1, pays 7:1 and it has a house edge of 11.1 percent.
– 2 and 12 Craps have odds of 35 to 1, pays 30:1 and it has a house edge of 13.9 percent.
– 3 and 11 Craps have odds of 17 to 1, pays 15:1 and it has a house edge of 11.1 percent.
British casinos are tightly regulated and they offer better payouts on some of the best.
Craps Strategy
Craps is a dice game in which players will entirely either win or lose depending on the outcome of the dice. There isn’t any skill or decision making involved in the game — it is purely based on luck. There are no strategies or techniques to this game either. Despite that, there are some betting tips that can help players minimize their losses and increase their odds.
If you are a beginner, it is better to stick to the Pass Line Bet because the house edge of this wager equals 1.41 percent. The rest of the Craps bets at the table offer worse odds, so this is the best bet for new players. Although the Do Not Pass offers better odds as it has a house edge of 1.36 percent, it is frowned upon because you will be betting against the shooter and people will not appreciate that. It is safer to bet on the Pass Line wager because you wouldn’t want to antagonize and cross the shooter for a small 0.05 percent advantage.
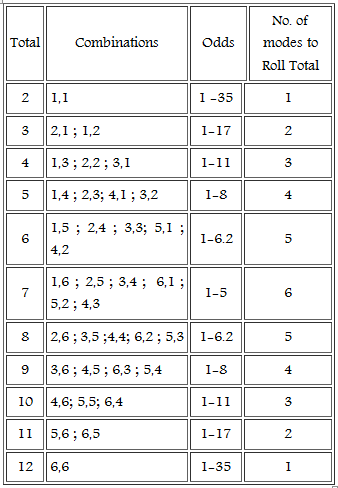
Craps Dice Probability Chart
The best bet in craps after the first roll is the odds bet. Once a point is determined, players will be able to place an additional wager that is a multiple of the pass line bet. The multiple differs from one casino to another, but the most common is 2X. The best thing about the odds bets is that it pays according to their true odds, which means the house has a 0% advantage; players should always place these bets.
Stay away from the proposition bets. These bets are settled in one roll.
Although the dealer might tempt you to place these bets, you should not because they have the highest house advantage.
Players are also advised to tip the dealers at the Craps tables. This is not a bribe — in no way can the dealer interfere or affect the outcome of the dice. On the other hand, they can guide you and help you throughout the game. Dealers rely on these tips and they are a great part of their salary. Tipping the dealer will create a repoire and you will receive invaluable advice that will help elevate the level of your game.
Players should also read about the etiquette and learn the unwritten rules of Craps are. Some casinos will give players the boot and request that they leave if they are not following and abiding by these etiquette rules. You can find out more about these rules at the “Rules” section of Craps on this website.
Lastly, players are advised against taking tips from other players at the Craps table, no matter how tempting it might be, because the other players will not always give the correct advice.
Pro’s Perspective: Craps Strategies and Tips
With John Grochowski
Players who take the house edge seriously will quickly come to the conclusion that only a few bets are worth taking. Pass or do not pass and come or do not come are the basics, and some players also like place bets on 6 or 8 despite a slightly higher house edge just so that they can get the most frequently rolled non-7s working for them.
One-roll Bets and House Edge
One roll bets aren’t worth a second look. Why settle for an 11.1 percent house edge on any craps when you can bet pass at 1.41 percent? Given that a player is sticking with the best bets, the next question to arise often is, “Should I take the odds?” The answer depends on your bankroll and bet size.
There is no house edge on the odds. Paying at true odds, they’re a rare example of even bets in a casino. To take the odds, however, you must bet pass or come, or don’t pass or don’t come, and those bets do carry an edge. If you’re a table minimum bettor, it’s between you and your bankroll as to whether you take the odds.
The Reality of Craps Odds
Let’s say you’re at a table with a $5 minimum bet, and you bet that minimum on the pass line 100 times. You have $500 at risk. The 1.414 percent house edge means that at the end of the trial, the average house take from your $500 is $7.07.
Now let’s say you bet the $5 minimum on a pass and $10 in double odds. Per 100 trials, you risk $500 on a pass and $1,000 double odds. The odds are a break-even bet, so on average, the house take is zero, while the house take on your pass bets remains $7.07. When results deviate from average, you can have much larger wins when you take the odds, and also much larger losses. Your average loss comes back to that same $7.07 with or without odds.
Now let’s say you increase your pass bet to $15 without taking odds. Your risk per 100 trials increases to $150, and your average loss increase to $21.21.
Advantages to Taking Odds
Here’s where it’s to your advantage to take the odds. Instead of increasing your pass bet to $15, leave it at the table minimum of $5, then use the rest of your intended bet increase to take the odds. That leaves your average loss at $7.07 while opening the door to larger wins.
Many modern casinos offer more than double odds. Some offer up to 100x odds, and it’s become increasingly common for American casinos to offer 3x, 4x, 5x odds, meaning you can make an odds bet of three times your pass or come bet if the point number is 4 or 10, four times on 5 or 9 or five times on 6 or 8.
Regardless of what odds the casino permits, the most advantageous play is to use the odds bet to keep your pass or come bet low, then to put more of your money on the higher-paying odds.

Alter then so that one die has a six on every side, and the other one has all ones and fives.
Thanks for the kind words. No, I don't think that wishful thinking helps in the casino, all other things being equal.
The question on the dice influence is a hotly debated topic. Personally, I'm very skeptical. As I review this reply in 2013 I still have yet to see convincing evidence anybody can influence enough to have an advantage.
I'm very skeptical of it. I go over some of the experiments on the topic in my craps appendix 3.
I don’t believe in it. So far I have yet to see a name I respect endorse the method, nor any evidence that it works. While I don’t entirely rule out the possibility I am extremely skeptical of it. I may live in Nevada but when it comes to things like dice setting I’m from Missouri, 'show me' it works.
With ordinary dice, the like those you get in a board game, this is true. However casino dice have inlaid spots. At the factory they drill holes for the spots then insert white colored spots into the holes, of the same density as the die itself. So the die is essentially a perfect cube. Even if they did use ordinary dice from a board game I doubt the bias would be nearly enough to overcome the house edge.
I think there is no such thing as a naturally bad shooter. With the possible exception of a few pros all dice throws can be considered truly random. There are seminars on how to overcome the house edge in craps by precession throwing but I make no claims for or against them. I have yet to see enough evidence either way.
I lost the $1800 to another gambling writer, not Stanford. I would have preferred more rolls but there was an obvious time contraint. Assuming one throw per minute it would take 34.7 days to throw the dice 50,000 times. I wasn’t the one who decided on 500 but it seemed like a reasonable compromise between a large sample size and time. You are right that 500 is too few to make a good case for or against influencing the dice, but 500 throws is better than zero.
For large numbers of throws we can use the Gaussian Curve approximation. The expected number of sevens in 655 throws is 655 × (1/6) = 109.1667. The variance is 655 × (1/6) × (5/6) = 90.9722. The standard deviation is sqr(90.9722) = 9.5379. Your 78 sevens is 109.1667 − 78 = 31.1667 less than expectation. This is (31.1667 - 0.5)/9.5379 = 3.22 standard deviations below expectation. The probability of falling 3.22 or more standard deviations south of expectations is 0.000641, or 1 in 1,560. I got this figure in Excel, using the formula, normsdist(-3.22).
This is about controlling the dice at Craps. You previously discussed the Stanford Wong Experiment, stating, 'The terms of the bet were whether precision shooters could roll fewer than 79.5 sevens in 500 rolls of the dice. The expected number in a random game would be 83.33. The probability of rolling 79 or fewer sevens in 500 random rolls is 32.66%.... The probability of rolling 74 or fewer sevens in 500 random rolls is 14.41%.'The question I have about this bet is that 14.41% still isn’t 'statistically significant' [ i.e. p < 0.05 ] , which is usually taken to mean greater than two Standard Deviations from the Mean -- or a probability of less than a *combined* 5% of the event happening randomly on EITHER end of the series.
How many Sevens would have to be rolled in 500 rolls before you could say that there is a less than 2.5% chance that the outcome was entirely random (i.e. that the outcome was statistically significant) ?
Many Thanks & BTW , yours is ABSOLUTELY the BEST web site on the subject of gambling odds & probabilities that I’ve found .... keep up the good work !!!
Thank you for the kind words. You should not state the probability that the throws were non-random is p. The way it should be phrased is the probability that a random game would produce such a result is p. Nobody expected 500 rolls to prove or disprove anything. It wasn’t I who set the line at 79.5 sevens, but I doubt it was chosen to be statistically significant; but rather, I suspect the it was a point at which both parties would agree to the bet.
The 2.5% level of significance is 1.96 standard deviations from expectations. This can be found with the formula =normsinv(0.025) in Excel. The standard deviation of 500 rolls is sqr(500*(1/6)*(5/6)) = 8.333. So 1.96 standard deviations is 1.96 * 8.333 = 16.333 rolls south of expectations. The expected number of sevens in 500 throws is 500*(1/6) = 83.333. So 1.96 standard deviations south of that is 83.333 − 16.333 = 67. Checking this using the binomial distribution, the exact probability of 67 or fewer sevens is 2.627%.
There is no definitive point at which confidence is earned. It is a matter of degree. First, I would ask what is being tested for, and what the shooter estimates will happen. With any test there are two possible errors. A skilled shooter might fail, because of bad luck, or a random shooter might pass because of good luck. Of the two, I would prefer to avoid a false positive. I think a reasonable test would set the probability of a false negative at about 5%, and a false positive at about 1%.
For example, suppose the claimant says he can average one total of seven every seven throws of the dice. A random shooter would throw one seven every six throws, on average. By trial and error I find that a test meeting both these criteria would be to throw the dice 3,600 times, and require 547 or fewer sevens to pass, or one seven per 6.58 rolls.
A one in seven shooter should average 514.3 sevens, with a standard deviation of 21.00. Using the Gaussian approximation, the probability of such a skilled shooter throwing 548 or more sevens (a false negative) is 5.7%. A random shooter should average 600 sevens, with a standard deviation of 22.36. The probability of a random shooter passing the test (a false positive) is 0.94%. The graph below shows the possibe results for skilled and random shooters. If the results are to the left of the green line, then I would consider the shooter to have passed the test, and I would bet on him.
The practical dilemma is if we assume two throws per minute, it would take 30 hours to conduct the test. Perhaps I could be more liberal about the significance level, to cut down the time requirement, but the results would not be as convincing. I do think the time has come for a bigger test than the 500-roll Wong experiment.
First of all, she rolled the dice a total of 154 times, with the 154th roll being a seven out (Source: NJ.com). However, that does not mean she never rolled a seven in the first 153 rolls. She could have rolled lots of them on come out rolls. As I show in my May 3, 2003 column, the probability of making it to the 154th roll is 1 in 5.6 billion. The odds of winning Mega Millions are 1 in combin(56,5)*46 = 175,711,536. So going 154 rolls or more is about 32 times as hard. Given enough time and tables, which I think exist, something like this was bound to happen sooner or later. So, I wouldn't suspect cheating. I roughly estimate the probability that this happens any given year to be about 1%.
Also see my solution, expressed in matrices, at mathproblems.info, problem 204.
I think some of the casinos in Las Vegas are using dice that are weighted on one side. As evidence, I submit the results of 244 throws I collected at a Strip casino. What are the odds results this skewed could come from fair dice?| Dice Test Data | |
| Dice Total | Observations |
| 2 | 6 |
| 3 | 12 |
| 4 | 14 |
| 5 | 18 |
| 6 | 23 |
| 7 | 50 |
| 8 | 36 |
| 9 | 37 |
| 10 | 27 |
| 11 | 14 |
| 12 | 7 |
| Total | 244 |
7.7%.
The chi-squared test is perfectly suited to this kind of question. To use the test, take (a-e)2/e for each category, where a is the actual outcome, and e is the expected outcome. For example, the expected number of rolls totaling 2 in 244 throws is 244×(1/36) = 6.777778. If you don’t understand why the probability of rolling a 2 is 1/36, then please read my page on dice probability basics. For the chi-squared value for a total of 2, a=6 and e=6.777778, so (a-e)2/e = (6-6.777778)2/6.777778 = 0.089253802.
Chi-Squared Results
| Dice Total | Observations | Expected | Chi-Squared |
| 2 | 6 | 6.777778 | 0.089253 |
| 3 | 12 | 13.555556 | 0.178506 |
| 4 | 14 | 20.333333 | 1.972678 |
| 5 | 18 | 27.111111 | 3.061931 |
| 6 | 23 | 33.888889 | 3.498725 |
| 7 | 50 | 40.666667 | 2.142077 |
| 8 | 36 | 33.888889 | 0.131512 |
| 9 | 37 | 27.111111 | 3.607013 |
| 10 | 27 | 20.333333 | 2.185792 |
| 11 | 14 | 13.555556 | 0.014572 |
| 12 | 7 | 6.777778 | 0.007286 |
| Total | 244 | 244 | 16.889344 |
Chance Of Winning Craps
Then take the sum of the chi-squared column. In this example, the sum is 16.889344. That is called the chi-squared statistic. The number of 'degrees of freedom' is one less than the number of categories in the data, in this case 11-1=10. Finally, either look up a chi-squared statistic of 10.52 and 10 degrees of freedom in a statistics table, or use the formula =chidist(16.889344,10) in Excel. Either will give you a result of 7.7%. That means that the probability fair dice would produce results this skewed or more is 7.7%. The bottom line is while these results are more skewed than would be expected, they are not skewed enough to raise any eyebrows. If you continue this test, I would suggest collecting the individual outcome of each die, rather than the sum. It should also be noted that the chi-squared test is not appropriate if the expected number of outcomes of a category is low. A minimum expectation of 5 is a figure commonly bandied about.
Whether or not it is called a valid roll depends on where you are. New Jersey gaming regulation 19:47-1.9(a) states:
A roll of the dice shall be invalid whenever either or both of the dice go off the table or whenever one die comes to rest on top of the other. -- NJ 19:47-1.9(a)
Pennsylvania has the exact same regulation, Section 537.9(a):
A roll of the dice shall be invalid whenever either or both of the dice go off the table or whenever one die comes to rest on top of the other. -- PA 537.9(a)
I asked a Las Vegas dice dealer who said that here it would be called a valid roll, if it was otherwise a proper throw. Although he has never seen it happen, he said if it did the dealers would simply move the top die to see what number the lower die landed on. However, one can determine the outcome of the lower die without touching, or looking through, the top die. Here is how to do it. First, by looking at the four sides you can narrow down the possibilities on top to two. Here is how to tell according to the three possibilities.
- 1 or 6: Look for the 3. If the high dot is bordering the 5, the 1 is on top. Otherwise, if it is bordering the the 2, the 6 is on top.
- 2 or 5: Look for the 3. If the high dot is bordering the 6, the 2 is on top. Otherwise, if it is bordering the the 1, the 5 is on top.
- 3 or 4: Look for the 2. If the high dot is bordering the 6, the 3 is on top. Otherwise, if it is bordering the the 1, the 4 is on top.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
This question was asked at TwoPlusTwo.com, and was answered correctly by BruceZ. The following solution is the same method as that of BruceZ, who deserves proper credit. It is a difficult answer, so pay attention.
First, consider the expected number of rolls to obtain a total of two. The probability of a two is 1/36, so it would take 36 rolls on average to get the first 2.
Next, consider the expected number of rolls to get both a two and three. We already know it will take 36 rolls, on average, to get the two. If the three is obtained while waiting for the two, then no additional rolls will be needed for the 3. However, if not, the dice will have to be rolled more to get the three.
The probability of a three is 1/18, so it would take on average 18 additional rolls to get the three, if the two came first. Given that there is 1 way to roll the two, and 2 ways to roll the three, the chances of the two being rolled first are 1/(1+2) = 1/3.
So, there is a 1/3 chance we'll need the extra 18 rolls to get the three. Thus, the expected number of rolls to get both a two and three are 36+(1/3)×18 = 42.
Next, consider how many more rolls you will need for a four as well. By the time you roll the two and three, if you didn't get a four yet, then you will have to roll the dice 12 more times, on average, to get one. This is because the probability of a four is 1/12.
What is the probability of getting the four before achieving the two and three? First, let's review a common rule of probability for when A and B are not mutually exclusive:
pr(A or B) = pr(A) + pr(B) - pr(A and B)
You subtract pr(A and B) because that contingency is double counted in pr(A) + pr(B). So,
pr(4 before 2 or 3) = pr(4 before 2) + pr(4 before 3) - pr(4 before 2 and 3) = (3/4)+(3/5)-(3/6) = 0.85.
The probability of not getting the four along the way to the two and three is 1.0 - 0.85 = 0.15. So, there is a 15% chance of needing the extra 12 rolls. Thus, the expected number of rolls to get a two, three, and four is 42 + 0.15*12 = 43.8.
Next, consider how many more rolls you will need for a five as well. By the time you roll the two to four, if you didn't get a five yet, then you will have to roll the dice 9 more times, on average, to get one, because the probability of a five is 4/36 = 1/9.
What is the probability of getting the five before achieving the two, three, or four? The general rule is:
pr (A or B or C) = pr(A) + pr(B) + pr(C) - pr(A and B) - pr(A and C) - pr(B and C) + pr(A and B and C)
So, pr(5 before 2 or 3 or 4) = pr(5 before 2)+pr(5 before 3)+pr(5 before 4)-pr(5 before 2 and 3)-pr(5 before 2 and 4)-pr(5 before 3 and 4)+pr(5 before 2, 3, and 4) = (4/5)+(4/6)+(4/7)-(4/7)-(4/8)-(4/9)+(4/10) = 83/90. The probability of not getting the four along the way to the two to four is 1 - 83/90 = 7/90. So, there is a 7.78% chance of needing the extra 7.2 rolls. Thus, the expected number of rolls to get a two, three, four, and five is 43.8 + (7/90)*9 = 44.5.
Continue with the same logic, for totals of six to twelve. The number of calculations required for finding the probability of getting the next number before it is needed as the last number roughly doubles each time. By the time you get to the twelve, you will have to do 1,023 calculations.
Here is the general rule for pr(A or B or C or ... or Z)
pr(A or B or C or ... or Z) =
pr(A) + pr(B) + ... + pr(Z)
- pr (A and B) - pr(A and C) - ... - pr(Y and Z) Subtract the probability of every combination of two events
+ pr (A and B and C) + pr(A and B and D) + ... + pr(X and Y and Z) Add the probability of every combination of three events
- pr (A and B and C and D) - pr(A and B and C and E) - ... - pr(W and X and Y and Z) Subtract the probability of every combination of four eventsThen keep repeating, remembering to add probability for odd number events and to subtract probabilities for an even number of events. This obviously gets tedious for large numbers of possible events, practically necessitating a spreadsheet or computer program.
The following table shows the the expected number for each step along the way. For example, 36 to get a two, 42 to get a two and three. The lower right cell shows the expected number of rolls to get all 11 totals is 61.217385.
Expected Number of Rolls Problem
| Highest Number Needed | Probability | Expected Rolls if Needed | Probability not Needed | Probability Needed | Expected Total Rolls |
|---|---|---|---|---|---|
| 2 | 0.027778 | 36.0 | 0.000000 | 1.000000 | 36.000000 |
| 3 | 0.055556 | 18.0 | 0.666667 | 0.333333 | 42.000000 |
| 4 | 0.083333 | 12.0 | 0.850000 | 0.150000 | 43.800000 |
| 5 | 0.111111 | 9.0 | 0.922222 | 0.077778 | 44.500000 |
| 6 | 0.138889 | 7.2 | 0.956044 | 0.043956 | 44.816484 |
| 7 | 0.166667 | 6.0 | 0.973646 | 0.026354 | 44.974607 |
| 8 | 0.138889 | 7.2 | 0.962994 | 0.037006 | 45.241049 |
| 9 | 0.111111 | 9.0 | 0.944827 | 0.055173 | 45.737607 |
| 10 | 0.083333 | 12.0 | 0.911570 | 0.088430 | 46.798765 |
| 11 | 0.055556 | 18.0 | 0.843824 | 0.156176 | 49.609939 |
| 12 | 0.027778 | 36.0 | 0.677571 | 0.322429 | 61.217385 |
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
The Wizard says that website sounds like a lot of ranting and raving with no credible evidence whatsoever to justify the accusation. I'd be happy to expose any casino for using biased dice, if I had any evidence of it.
If anybody has legitimate evidence of biased dice, I'd be happy to examine it and publish my conclusions. Evidence I would like to see are either log files of rolls or, better yet, some actual alleged biased dice.
Furthermore, if the casinos really were using dice that produced more than the expected number of sevens, then why aren't these detectives privy to the conspiracy out there betting the don't pass and laying the odds?
- 2 or 12: 1,000
- 3 or 11: 600
- 4 or 10: 400
- 5 or 9: 300
- 6 or 8: 200
My question is what is average bonus win?
Click the following button for the answer.
Click the following button for the solution.
Let x be the answer. As long as the player doesn't roll a seven he can always expect future wins to be x, in addition to all previous wins. In other words, there is a memory-less property to throwing dice in that no matter how many rolls you have already thrown you are no closer to a seven than you were when you started.I won't go into the basics of dice probabilities but just say the probability of each total is as follows:
- 2: 1/36
- 3: 2/36
- 4: 3/36
- 5: 4/36
- 6: 5/36
- 7: 6/36
- 8: 5/36
- 9: 4/36
- 10: 3/36
- 11: 2/36
- 12: 1/36
Before considering the consolation prize, the value of x can be expressed as:
x = (1/36)*(1000 + x) + (2/36)*(600 + x) + (3/36)*(400 + x) + (4/36)*(300 + x) + (5/36)*(200 + x) + (5/36)*(200 + x) + (4/36)*(300 + x) + (3/36)*(400 + x) + (2/36)*(600 + x) + (1/36)*(1000 + x)Next, multiply both sides by 36:
36x = (1000 + x) + 2*(600 + x) + 3*(400 + x) + 4*(300 + x) + 5*(200 + x) + 5*(200 + x) + 4*(300 + x) + 3*(400 + x) + 2*(600 + x) + (1000 + x)36x = 11,200 + 30x
Craps Odds And Probabilities - Craps:DICE CONTROL
6x = 11,200
Cached
x = 11,200/6 = 1866.67.Craps Dice Odds
Next, the value of the consolation prize is 700*(6/36) = 116.67.Thus, the average win of the bonus is 1866.67 + 116.67 = 1983.33.